Trabajo
Práctico N° 1
EL PLANO
CARTESIANO O EJES CARTESIANOS
Es un método matemático
para ubicar objetos en el plano mediante el uso de ejes y coordenadas.
Para ubicar puntos en el
plano es necesario usar dos referencias. Cada una de ellas se llama coordenada.
La primera coordenada
suele marcarse en el eje horizontal y se la denomina coordenada “X” o abscisa.
La otra coordenada es la
coordenada “y” u ordenada y se marca en el eje vertical.
La ubicación del par (a;b) está
determinada por la intersección entre la ubicación a en el eje x y la ubicación
b en el eje y. Por ejemplo si el par es (2;
4):
El par de puntos (2; 4) se denomina par ordenado; la primera componente se llama ordenada, y corresponde a x;
la segunda se llama ordenada, y
corresponde a y.
Concepto de Función.
Una función es una relación en la que a cada elemento de la variable
independiente le corresponde un solo elemento de la variable dependiente.
Una función se puede
representar gráficamente en un sistema de ejes cartesianos. En el siguiente gráfico se indica la distancia recorrida en función del tiempo:
Los valores
que toma la variable independiente forman el conjunto dominio y los valores que toma la variable dependiente forman el
conjunto imagen.
Formas
de expresar una función
Una
función puede expresarse mediante distintas maneras:
a) Un
Enunciado
Una
función se expresa a través de un enunciado cuando se describe verbalmente.
Por
ejemplo:
El
perímetro de un rectángulo es función de sus lados, base y altura. De forma que
la base de este rectángulo es el doble de la altura.
b) Una
tabla
Una
función se expresa a través de una tabla cuando se dan algunos valores de la
variable independiente x con los correspondientes a la variable dependiente y.
Por
ejemplo:
|
Tiempo en horas
|
1
|
2
|
3
|
4
|
|
Espacio recorrido
|
120
|
240
|
360
|
480
|
c) Una
Gráfica:
Una
función se expresa a través de una gráfica cuando se representan los pares (x,
y) en un sistema de ejes cartesianos. Como por ejemplo:
d) Una
Fórmula:
Una
función se expresa a través de una fórmula o expresión algebraica cuando se da
una ecuación que relaciona algebraicamente las dos variables que intervienen.
Como
por ejemplo:
Un
tren lleva una velocidad constante de 120 km/h, entonces la correspondencia
entre el espacio recorrido y el tiempo transcurrido es una función expresada
mediante la fórmula: e= 120.t
Funciones Afines y Funciones Lineales.
Diferencia entre ambas funciones
Las funciones
lineales, son aquellas funciones de proporcionalidad directa, es decir son
aquellas funciones en las cuales las variables aumentan o disminuyen de manera
proporcional (si aumenta una variable la otra también o si disminuye una la
otra lo hace de la misma manera). Estas funciones son de la forma F(x)= ax O y= ax. Se llaman también
funciones de proporcionalidad directa.
En cambio las
funciones afines son aquellas de la forma F(x)=
ax+b, donde tenemos el valor b, además
de la constante “a” que multiplica a
la “x”.
A estas
funciones le corresponde gráficamente una recta. La forma de la ecuación de una
recta es F(x)= “a”. x + “ b” o y =
“a” . x + “b” (Forma explícita). Donde “a” y “b” son dos números reales cualesquiera (Pero “a”
debe ser distinto de 0).
Para comenzar
a graficar Rectas, vamos a ir a un caso sencillo: y= 2x + 1
Donde “a”
vale 2 y “b” vale 1. Preparemos una tabla de valores: La tabla de valores tiene
2 columnas:
ü
En
la primer columna, inventamos los valores que le damos a la x. La variable x es independiente.
ü
En
la segunda columna, calculamos los valores que va tomando y según cada valor de x. La
variable y se llama variable dependiente.
|
Si x vale
|
Entonces y vale:
|
|
1
|
3 Reemplazamos
la “X” por 1 y calculamos lo que vale “Y”
|
Comencemos
asignándole a x el valor 1…
Partimos de
la fórmula de la ecuación de la recta:
y = 2.x +1 si
x = 1 y = 2. 1 + 1 = 3
Y probando
con otros puntos:
|
Si x vale
|
Entonces y vale:
|
Para calcular la
variable “Y” siempre reemplazamos “x” por el número que elegimos en cada
fila.
|
|
1
|
2 . 1 + 1 = 3
|
|
|
0
|
2 . 0 + 1 = 1
|
|
|
-2
|
2 . (-2) + 1 = -3
|
Graficamos
los puntos de la tabla:
Por último, unimos estos puntos y tenemos ya graficada
la recta.
Bueno, hasta
acá, vimos cómo graficar una recta haciendo la tablita de valores, esto siempre
es válido, incluso para graficar cualquier función, pero en el caso de las
rectas vamos a ver ahora una manera más directa y rápida de graficarlas, para
eso veamos primero en detalle la “ecuación
implícita de la recta”.
La ECUACIÓN
EXPLÍCITA de una recta tiene la forma: y = a.x+b
“a” es un número real al que llamamos pendiente de la recta.
“b” es otro número al que llamamos ordenada al origen.
Pendiente
y Ordenada al origen:
Vamos a ver ahora cómo graficar estas rectas en función del significado de la
letras “a” y “b” o sea de la pendiente y la ordenada al origen de las rectas.
La
Ordenada al Origen: Es
el valor que toma “y” cuando “x=0” y este valor nos indica donde la recta
corta al eje Y. (En la fórmula general la expresaremos como “b”)
La recta que graficamos antes era y= 2.x + 1 Ordenada al origen= 1
(corta al eje Y en 1)
Ordenada al Origen
La
Pendiente: Este valor
lo que nos indica es la inclinación de la recta (En la fórmula general la
expresamos como “a”)…
Veamos como graficar una recta a
partir de su pendiente.
Ejemplo: Grafiquemos la recta: y = 1/4.x-1
Lo primero que hacemos es ubicar la
ordenada al origen, porque sabemos que la recta va a cortar al eje Y en ese
punto, por lo tanto ya tenemos un punto de partida para graficar la recta.
Marcamos entonces el -1 sobre el eje Y (y a
partir de ese punto ubico otro punto según la pendiente)
Rectas Verticales y Horizontales:
Rectas Horizontales: La ecuación de la recta es: y = y1 (Donde  es el valor donde corta
al eje Y).
es el valor donde corta
al eje Y).
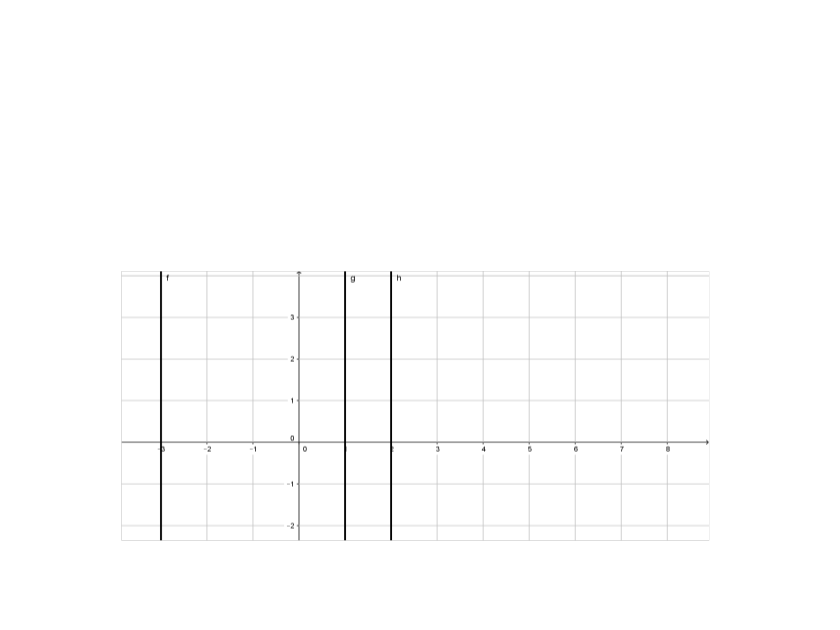
Rectas Verticales: La ecuación es: X = X1 (Donde  es el valor donde corta
al eje x)
es el valor donde corta
al eje x)
Para que una relación sea función debe cumplir dos condiciones:
ü
1)
A cada elemento del dominio le debe corresponder una única imagen.
ü
2)
En el dominio de la función no puede haber elementos que no posean imagen (o
sea no pueden quedar elementos libres).
Actividad:
Graficar las siguientes funciones, en un sistema de ejes cartesianos.
a) Y = 2x+1
b) Y= x+2
c) Y = 3x-1
Fecha de entrega: 08/04/2020









No hay comentarios:
Publicar un comentario